「算法笔记」Dijkstra

前言

• $SPFA​$算法由于它上限 $O(NM) = O(VE)​$的时间复杂度,被卡掉的几率很大.在算法竞赛中,我们需要一个更稳定的算法:$dijkstra​$.

什么是$dijkstra$?

• $dijkstra​$是一种单源最短路径算法,时间复杂度上限为$O(n^2)​$(朴素),在实际应用中较为稳定$;​$加上堆优化之后更是具有$O((n+m)\log_{2}n)​$的时间复杂度,在稠密图中有不俗的表现.

$dijkstra$的原理/流程?

• $dijkstra$本质上的思想是贪心,它只适用于不含负权边的图.
• 我们把点分成两类,一类是已经确定最短路径的点,称为”白点”,另一类是未确定最短路径的点,称为”蓝点”
• $dijkstra$的流程如下$:$
• $1.$ 初始化$dis[start] = 0,$其余节点的$dis$值为无穷大.
• $2.$ 找一个$dis$值最小的蓝点$x,$把节点$x$变成白点.
• $3.$ 遍历$x$的所有出边$(x,y,z),$若$dis[y] > dis[x] + z,$则令$dis[y] = dis[x] + z$
• $4.$ 重复$2,3$两步,直到所有点都成为白点$.$
• 时间复杂度为$O(n^2)$

$dijkstra$为什么是正确的

• 当所有边长都是非负数的时候,全局最小值不可能再被其他节点更新.所以在第$2$步中找出的蓝点$x$必然满足$:dis[x]$已经是起点到$x$的最短路径$.$我们不断选择全局最小值进行标记和拓展,最终可以得到起点到每个节点的最短路径的长度

图解

• (令$start = 1$)
• 开始时我们把$dis[start]$初始化为$0$,其余点初始化为$inf$
  
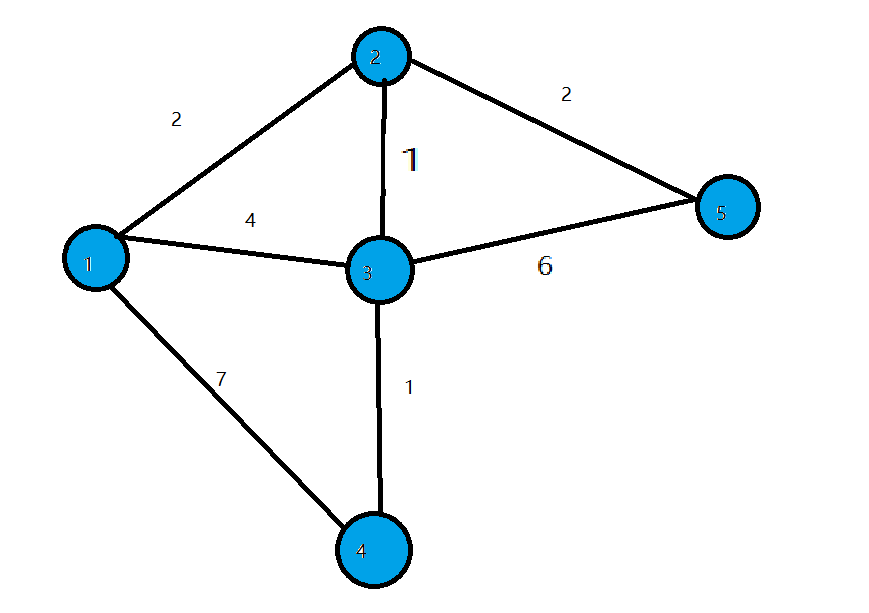
• 第一轮循环找到$dis$值最小的点$1$,将$1$变成白点,对所有与$1$相连的蓝点的$dis$值进行修改,使得$dis[2]=2,dis[3]=4,dis[4]=7$
  
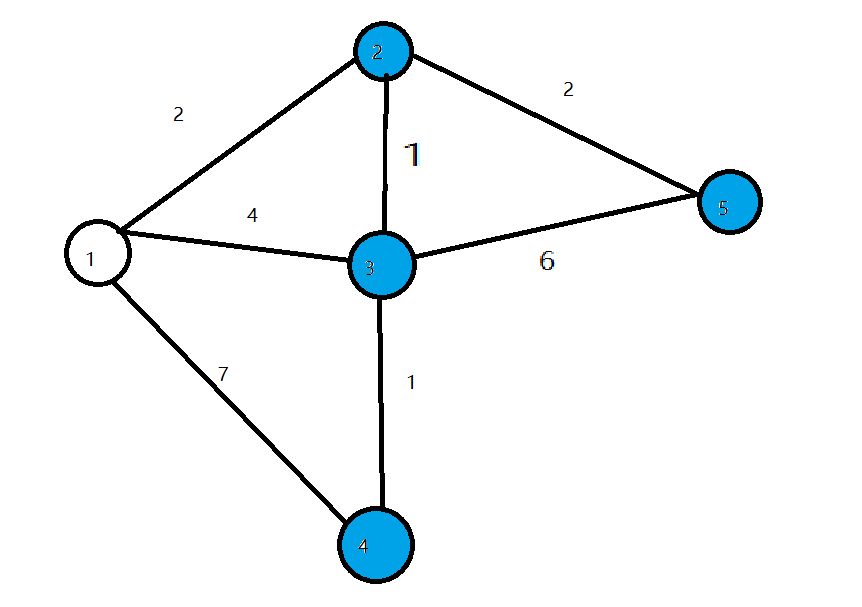
• 第二轮循环找到$dis$值最小的点$2$,将$2$变成白点,对所有与$2$相连的蓝点的$dis$值进行修改,使得$dis[3]=3,dis[5]=4$
  
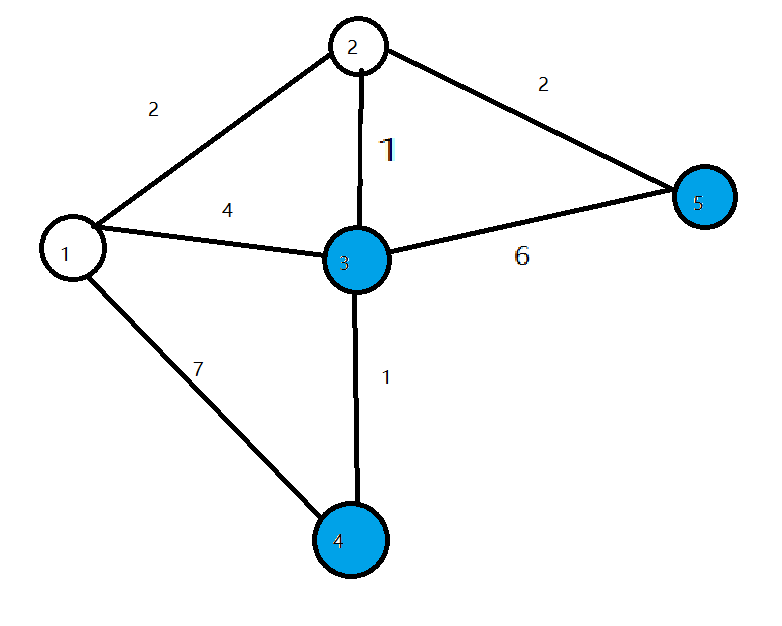
• 第三轮循环找到$dis$值最小的点$3$,将$3$变成白点,对所有与$2$相连的蓝点的$dis$值进行修改,使得$dis[4]=4$
  
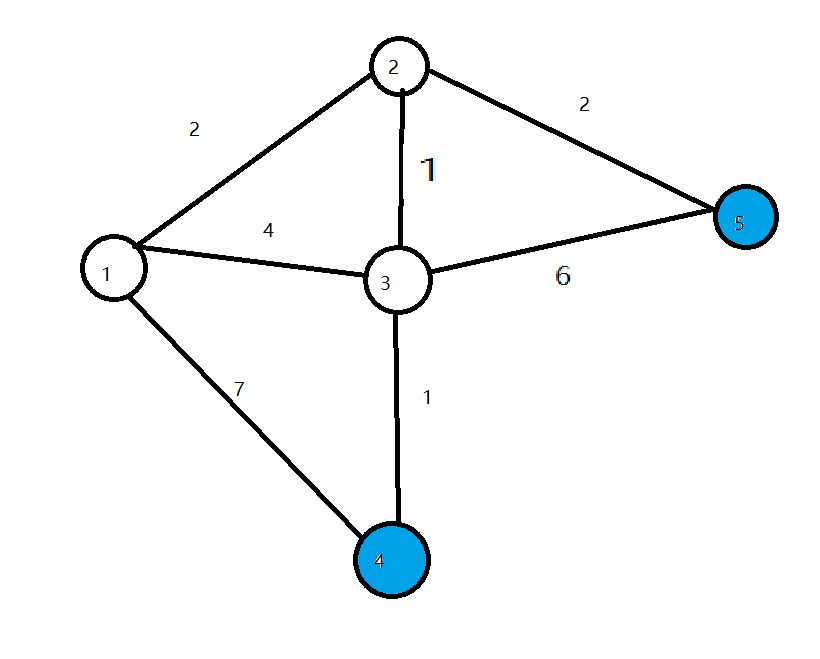
• 接下来两轮循环分别将$4,5$设为白点,算法结束,求出所有点的最短路径
• 时间复杂度$O(n^2)$

为什么$dijkstra$不能处理有负权边的情况?

• 我们来看下面这张图
  
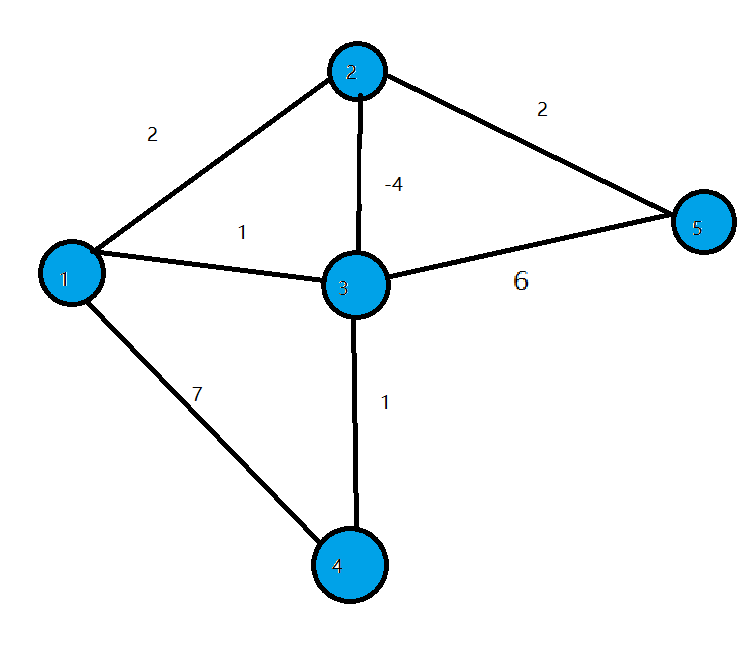
• $2$到$3$的边权为$-4$,显然从$1$到$3$的最短路径为$-2$ $(1->2->3).$但在循环开始时程序会找到当前$dis$值最小的点$3$,并标记它为白点.
• 这时的$dis[3]=1,$然而$1$并不是起点到$3$的最短路径.因为$3$已经被标为白点,所以$dis[3]$不会再被修改了.我们在边权存在负数的情况下得到了错误的答案.

$dijkstra$的堆优化?

• 观察$dijkstra$的流程,发现步骤$2$可以优化
• 怎么优化呢?
• 我会zkw线段树!我会斐波那契堆!
• 我会堆!

• 我们可以用堆对$dis$数组进行维护,用$O(\log_{2}n)$的时间取出堆顶元素并删除,用$O(\log_{2}n)$遍历每条边,总复杂度$O((n+m)\log_{2}n)$

• 范例代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79

#include<bits/stdc++.h>

const int MaxN = 100010, MaxM = 500010;

struct edge
{
    int to, dis, next;
};

edge e[MaxM];
int head[MaxN], dis[MaxN], cnt;
bool vis[MaxN];
int n, m, s;

inline void add_edge( int u, int v, int d )
{
    cnt++;
    e[cnt].dis = d;
    e[cnt].to = v;
    e[cnt].next = head[u];
    head[u] = cnt;
}

struct node
{
    int dis;
    int pos;
    bool operator <( const node &x )const
    {
        return x.dis < dis;
    }
};

std::priority_queue<node> q;


inline void dijkstra()
{
    dis[s] = 0;
    q.push( ( node ){0, s} );
    while( !q.empty() )
    {
        node tmp = q.top();
        q.pop();
        int x = tmp.pos, d = tmp.dis;
        if( vis[x] )
            continue;
        vis[x] = 1;
        for( int i = head[x]; i; i = e[i].next )
        {
            int y = e[i].to;
            if( dis[y] > dis[x] + e[i].dis )
            {
                dis[y] = dis[x] + e[i].dis;
                if( !vis[y] )
                {
                    q.push( ( node ){dis[y], y} );
                }
            }
        }
    }
}


int main()
{
    scanf( "%d%d%d", &n, &m, &s );
    for(int i = 1; i <= n; ++i)dis[i] = 0x7fffffff;
    for( register int i = 0; i < m; ++i )
    {
        register int u, v, d;
        scanf( "%d%d%d", &u, &v, &d );
        add_edge( u, v, d );
    }
    dijkstra();
    for( int i = 1; i <= n; i++ )
        printf( "%d ", dis[i] );
    return 0;
}

例题

• 入门模板:P3371
• 进阶模板:P4779
• 其余例题请右转洛谷 题库,搜索”最短路”

后记

• 本文部分内容摘自李煜东《算法竞赛进阶指南》和《信息学竞赛一本通》
• 友情提示:正权图请使用$dijkstra$算法,负权图请使用$SPFA$算法
• 感谢洛谷 各位管理员提供的平台