Overview
This assignment provides a comprehensive exploration of geometric modeling and mesh processing, implementing fundamental algorithms that form the backbone of modern computer graphics applications. The project spans two major areas: parametric curve and surface representation through Bezier curves, and triangle mesh manipulation using half-edge data structures.
In the first section, I implemented the de Casteljau algorithm for evaluating Bezier curves and surfaces, demonstrating how elegant recursive subdivision can generate smooth parametric shapes from simple control points. The second section delves into mesh editing operations, where I developed algorithms for computing area-weighted vertex normals, performing edge flips and splits, and implementing Loop subdivision for mesh upsampling.
What strikes me most about this assignment is how it bridges mathematical elegance with practical implementation challenges. The de Casteljau algorithm showcases the beauty of recursive geometric construction, while the half-edge mesh operations reveal the intricate bookkeeping required for maintaining topological consistency. The Loop subdivision algorithm particularly impressed me with its ability to transform coarse meshes into smooth surfaces through a carefully orchestrated sequence of local operations.
The most valuable lesson I learned is the importance of systematic approaches in geometric programming. Whether tracking half-edge pointers during mesh editing or managing iterator during subdivision, success depends on methodical organization and careful attention to data structure invariants. This assignment has deepened my appreciation for the sophisticated algorithms that enable the intuitive mesh editing tools we see in modern 3D modeling software.
Section 1: Bezier Curves and Surfaces
Part 1: Bezier Curves with 1D de Casteljau Subdivision
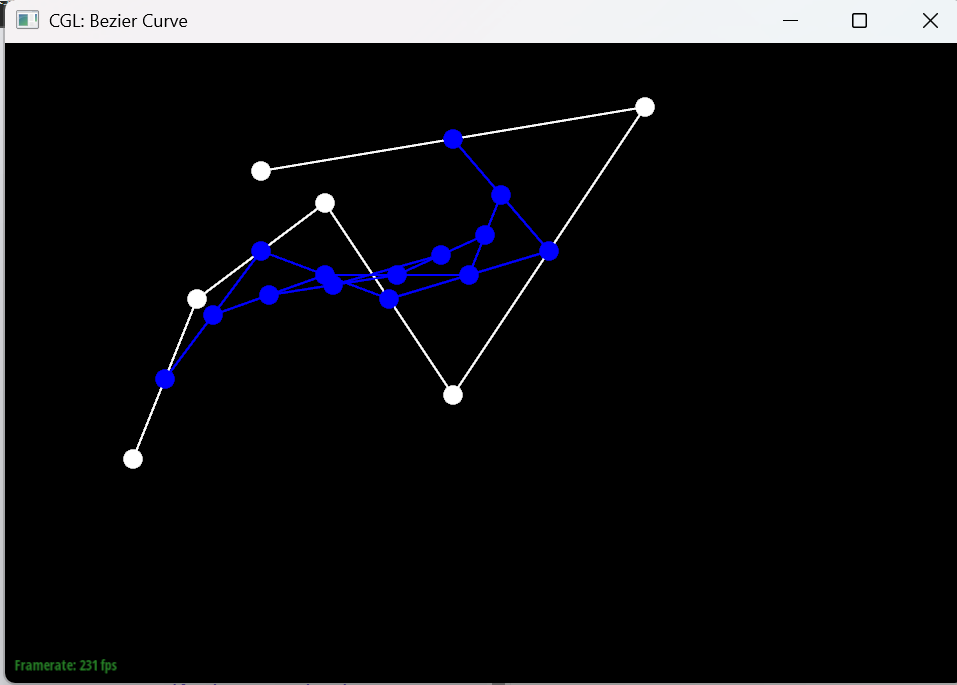
the de Casteljau algorithm is a recursive method for evaluating Bezier curves. It works by linearly interpolating between control points, and can be implemented in a straightforward manner using the provided evaluateStep function.
Screenshot
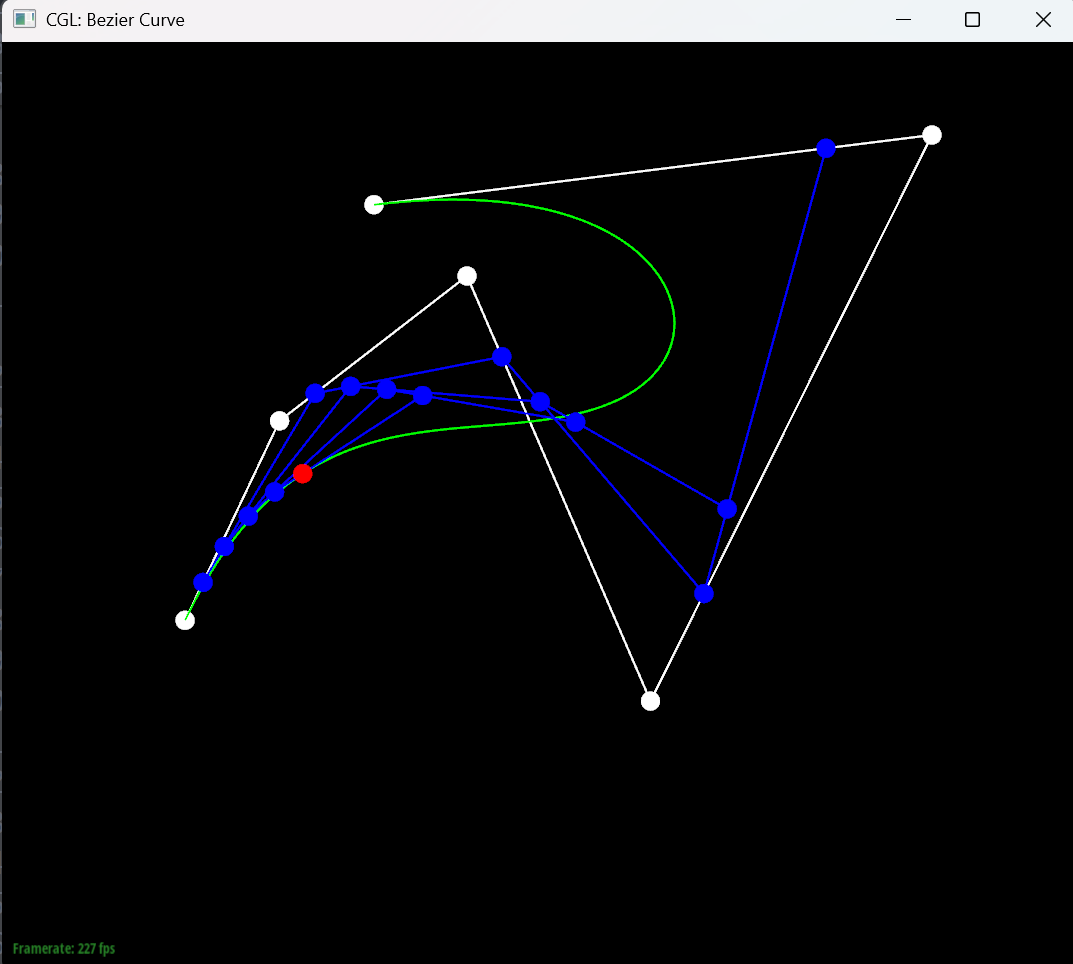
The following images show the results of evaluating two different Bezier curves using the implemented de Casteljau algorithm.
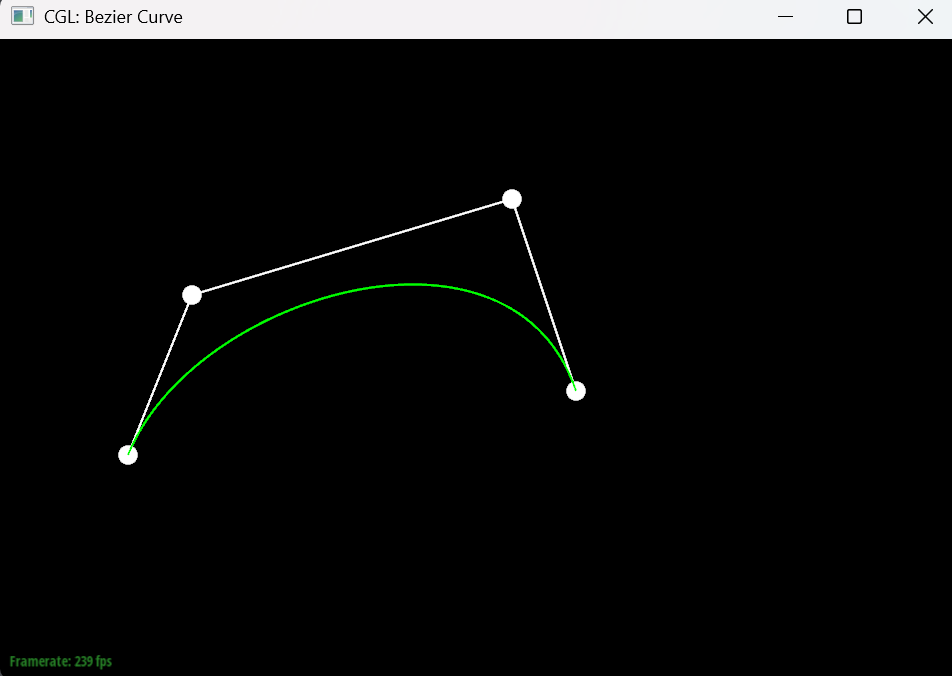
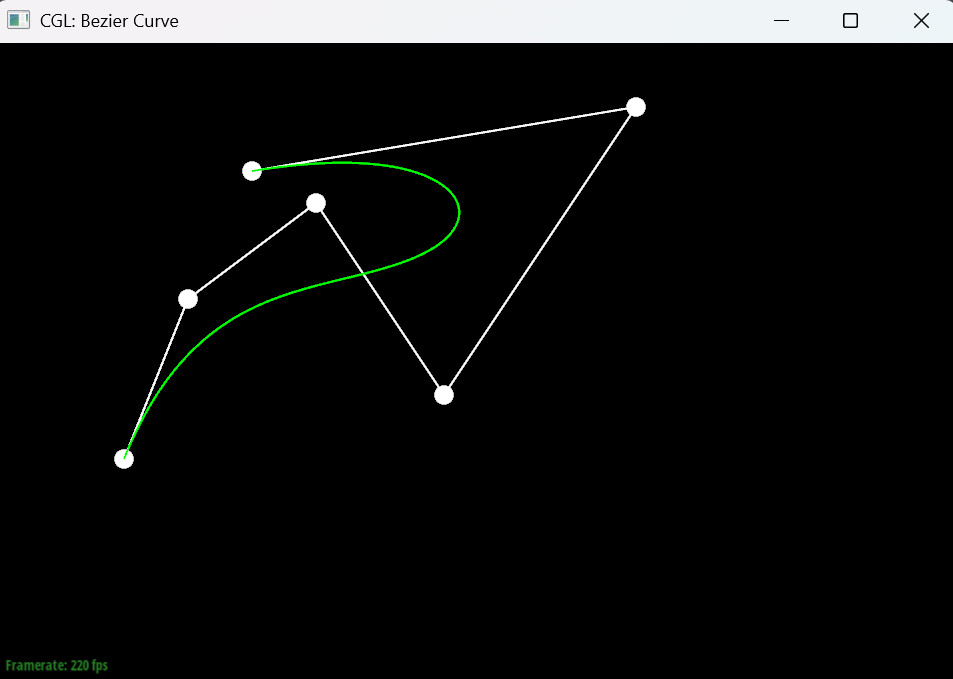
The following images shows the step-by-step subdivision of a Bezier curve.
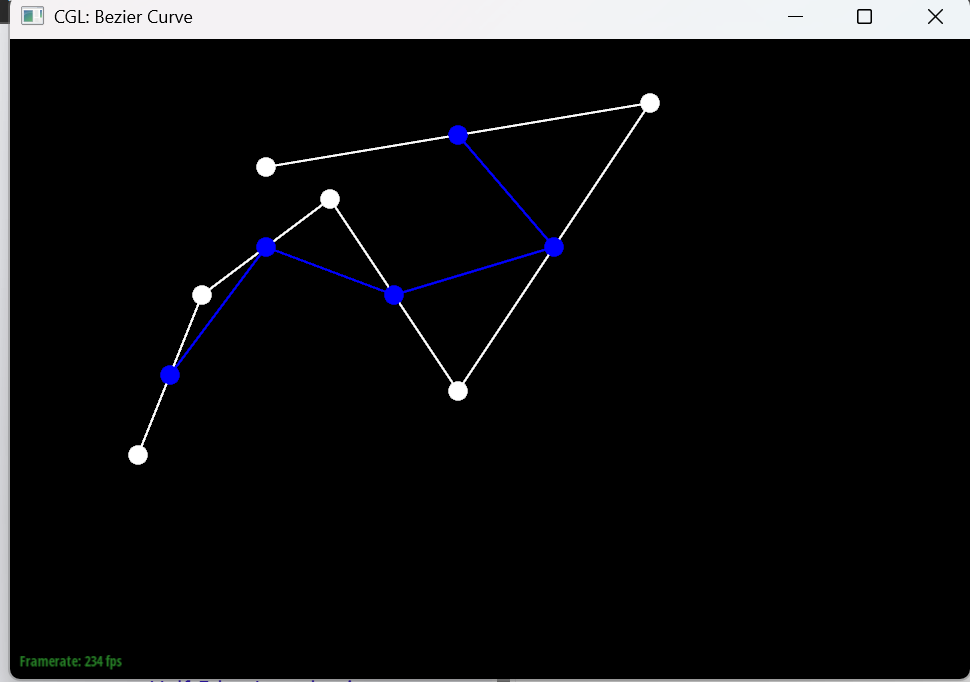
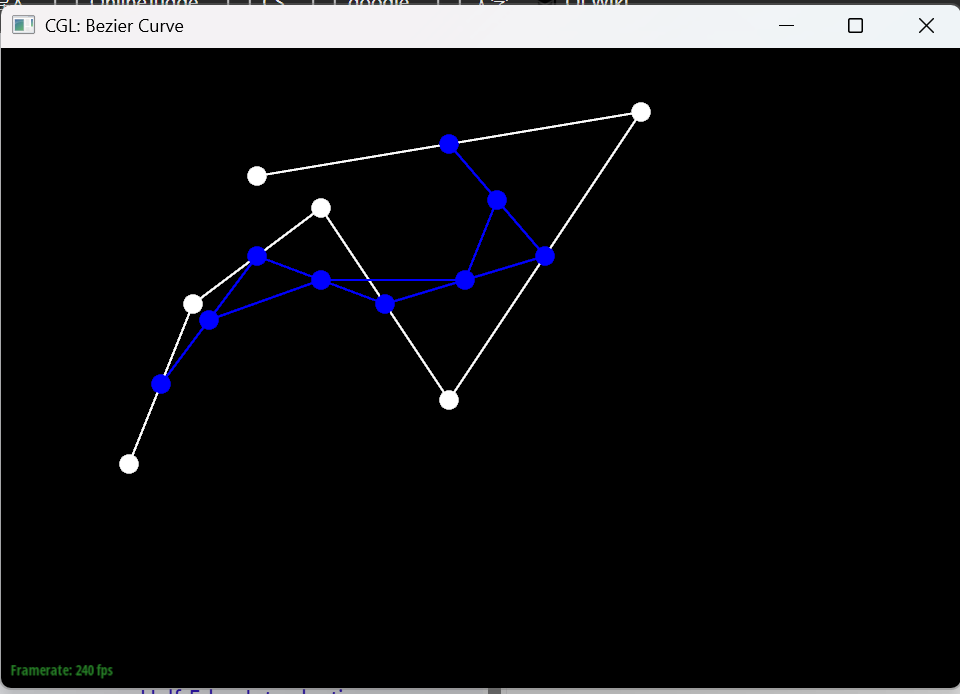
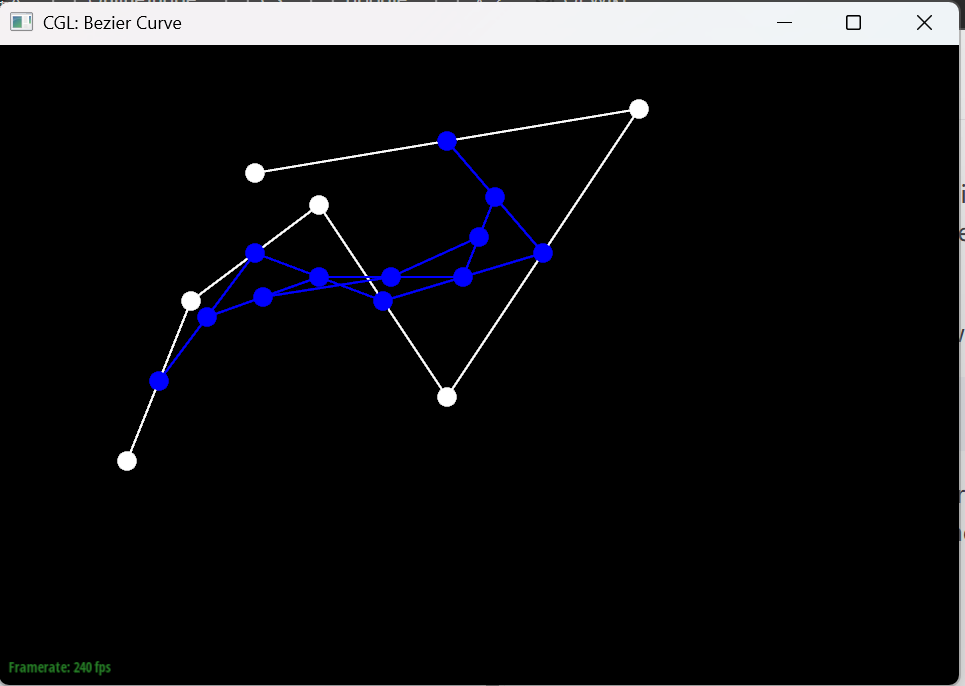
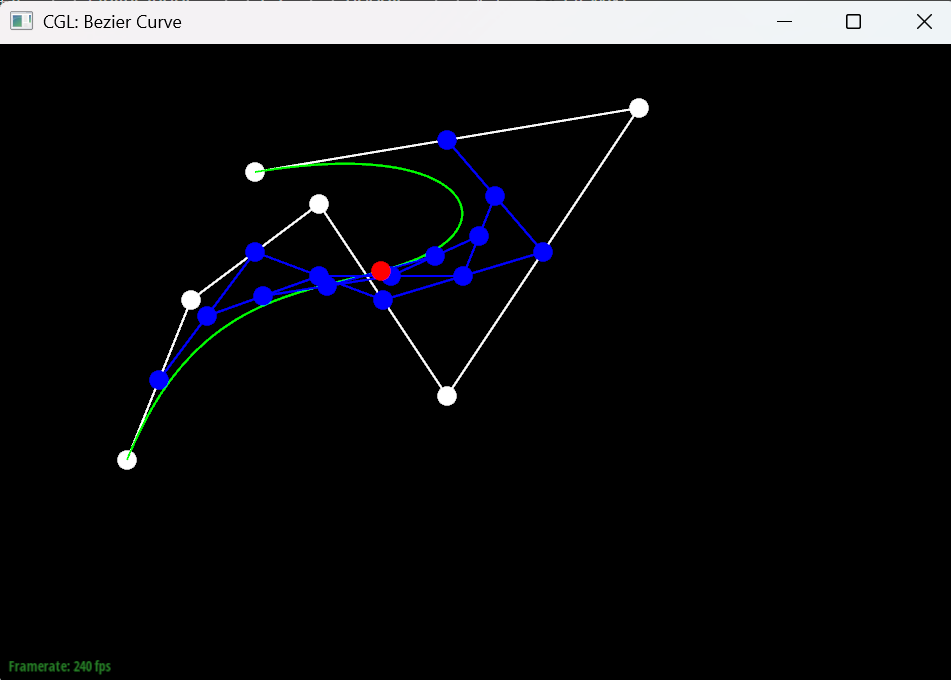
Here is a slightly different curve generated by dragging the control points and scrolling the mouse wheel to change the parameter t.
Part 2: Bezier Surfaces with Separable 1D de Casteljau
The Bezier surface evaluation is an extension of the 1D de Casteljau algorithm to two dimensions. The implementation involves evaluating the surface in one direction (u) and then in the other direction (v).
In my implementation, I first evaluate the Bezier curve in the u direction for each fixed v, resulting in a set of intermediate points. Then, I apply the de Casteljau algorithm again on these intermediate points in the v direction to obtain the final point on the Bezier surface.
Screenshot
The following images show the results of evaluating a Bezier surface using the implemented 2D de Casteljau algorithm.
Section II: Triangle Meshes and Half-Edge Data Structure
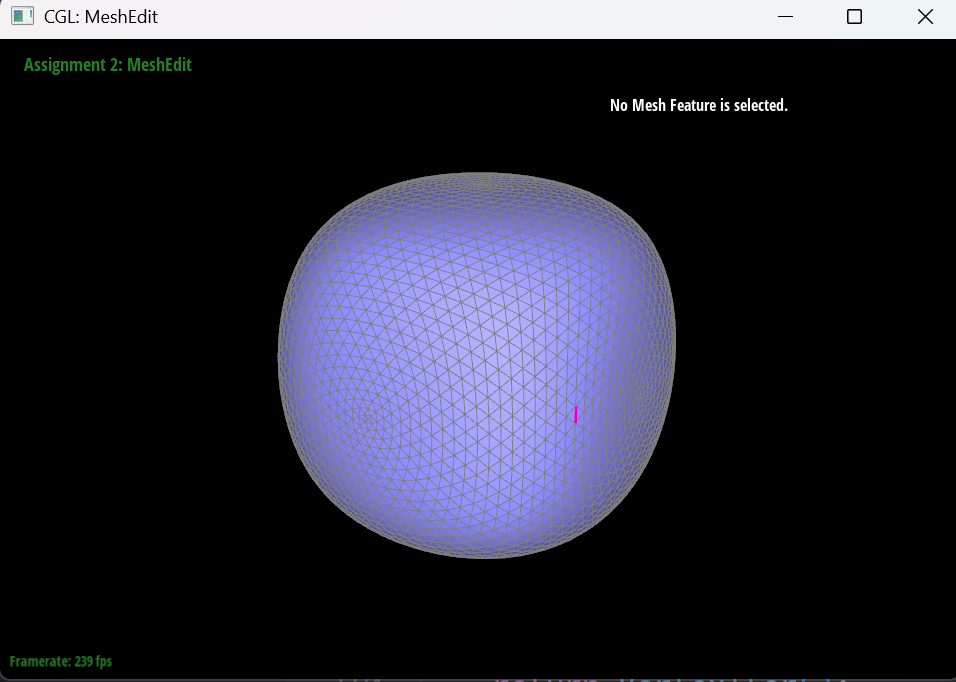
Part 3: Area-Weighted Vertex Normals
To compute the area-weighted vertex normals, I iterate all the faces adjacent to a vertex using a half-edge data structure. For each face, I compute the normal using the cross product of two edges of the face and weight it by the area of the face. The area can be computed as half the magnitude of the cross product of two edges. Finally, I normalize the accumulated normal vector to get the unit normal.
Screenshot
The following images show the vertex normals with the feature turned on and off.
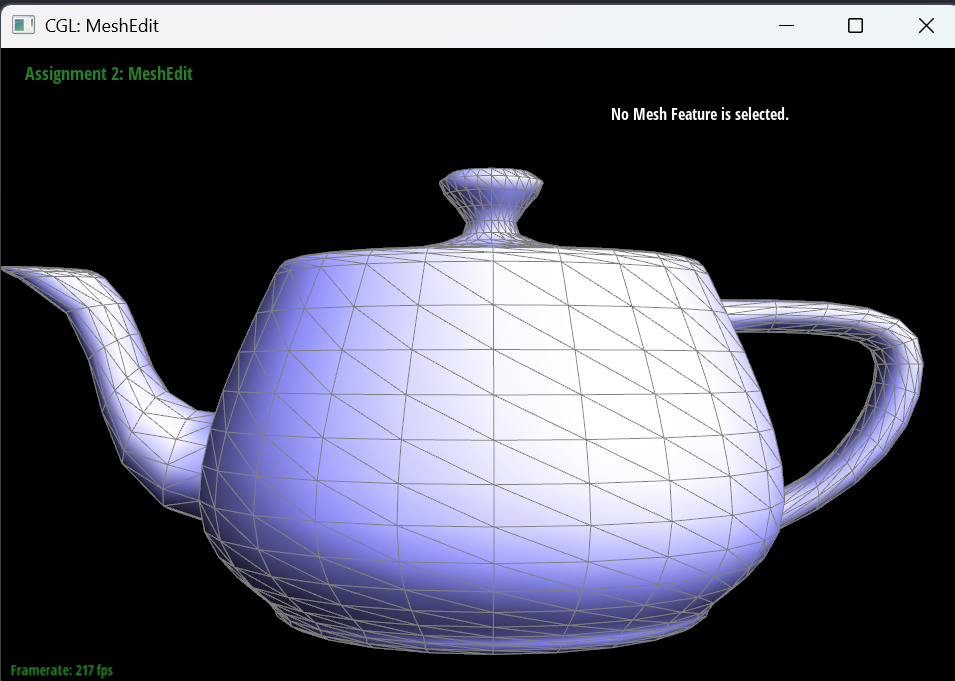
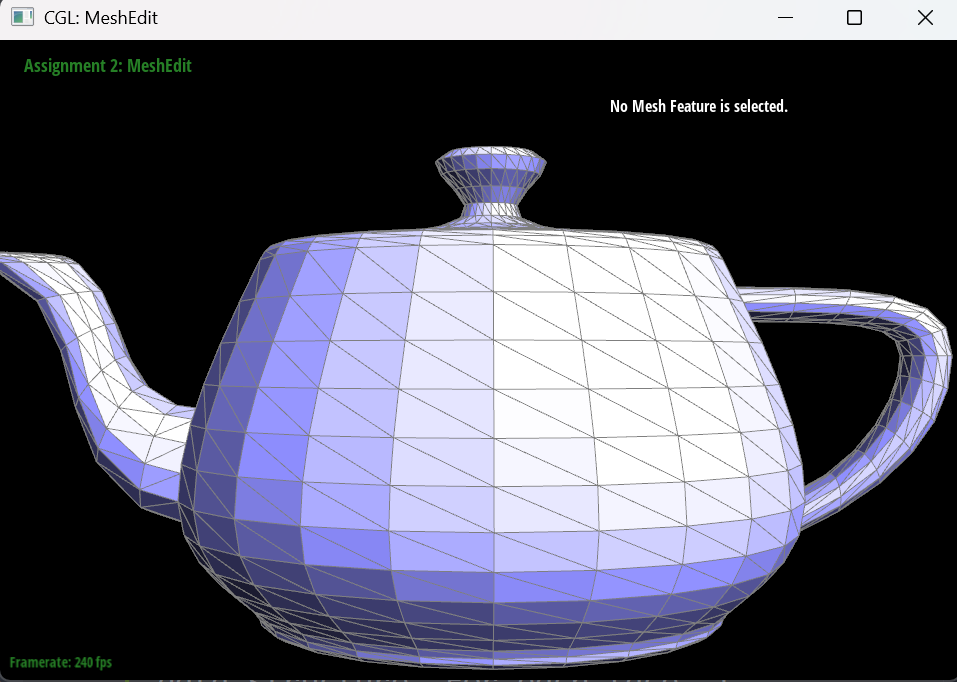
Part 4: Edge Flip
The edge flip operation transforms two adjacent triangles by flipping their shared edge. This is a fundamental operation in mesh editing that maintains the mesh’s topology while changing its geometry.
My implementation follows a systematic approach to ensure all half-edge data structure pointers are correctly updated. First, I verify that both faces adjacent to the edge are not boundary faces, as flipping boundary edges would create invalid topology. Then, I systematically collect all mesh elements involved in the flip operation: 6 halfedges forming the two triangles, 4 outer twin halfedges for the surrounding edges, 5 edges, 4 vertices, and 2 faces.
The key insight is to use the setNeighbors method to efficiently update all halfedge connections in a single call, which reduces the chance of errors compared to setting each pointer individually. After updating the halfedge topology, I update all back-pointers including twin relationships for outer edges, edge->halfedge pointers, vertex->halfedge pointers, and face->halfedge pointers to maintain consistency in the data structure.
Screenshot
This image shows the mesh before performing edge flip operations.
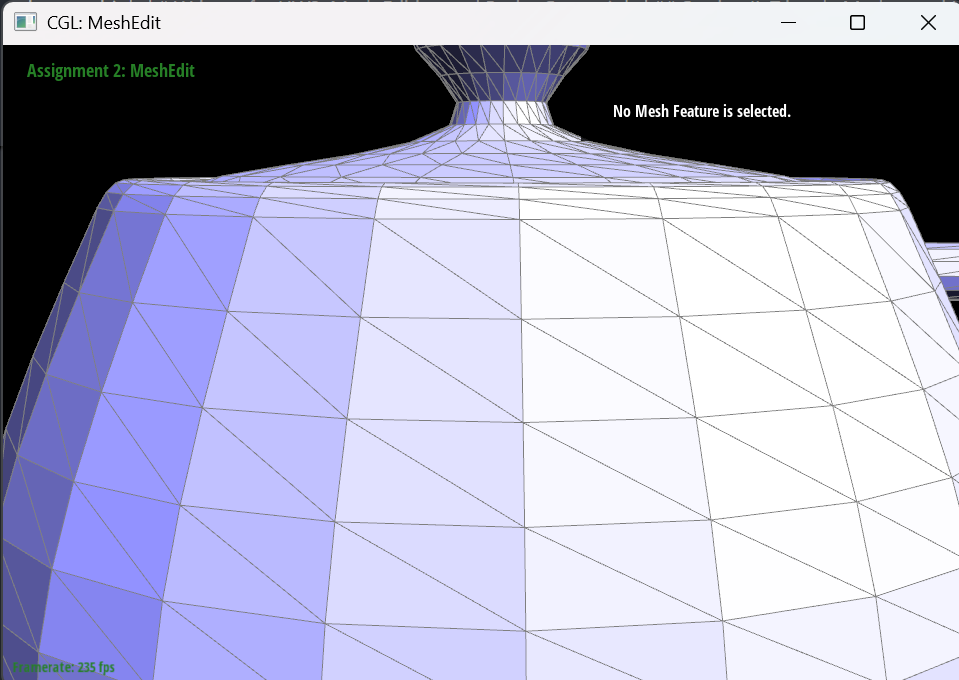
The following images show the mesh after performing edge flip operations.
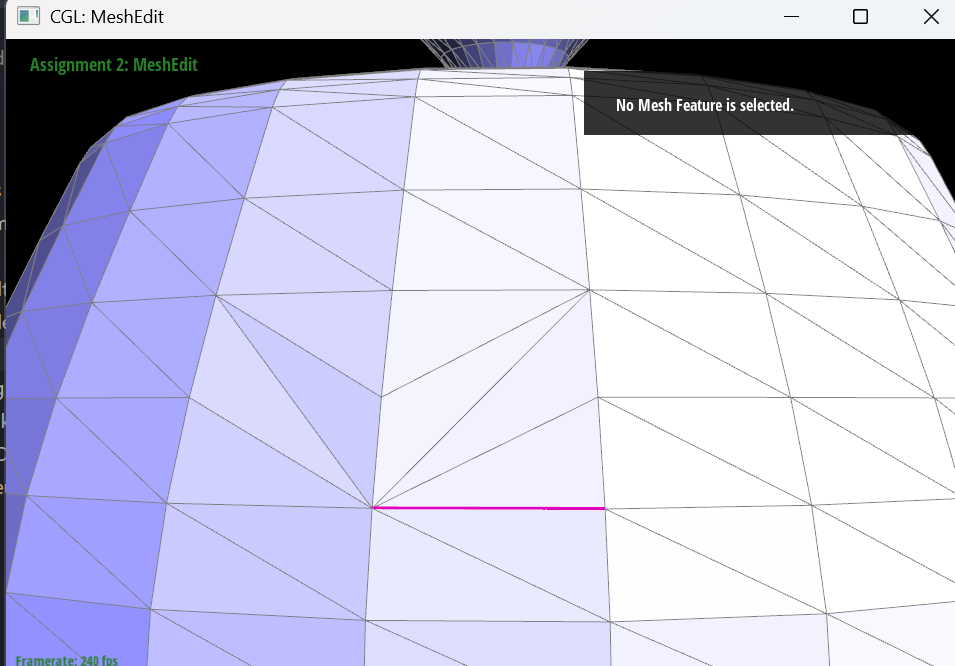
Part 5: Edge Split
The edge split operation divides an edge into two edges by inserting a new vertex at the midpoint. This operation transforms two adjacent triangles into four triangles, which is essential for mesh refinement and subdivision algorithms.
My implementation follows a similar systematic approach to the edge flip operation but is more complex due to the creation of new mesh elements. First, I verify that both faces adjacent to the edge are not boundary faces to ensure valid topology. Then, I collect all existing mesh elements: 6 halfedges forming the two triangles, 4 outer twin halfedges, 5 edges, 4 vertices, and 2 faces.
The key challenge is creating and properly connecting the new elements. I create a new vertex at the midpoint of the edge, three new edges to connect the midpoint to the opposite vertices, six new halfedges to form the additional triangular faces, and two new faces. The implementation uses the setNeighbors method to efficiently update all halfedge connections, ensuring that the four resulting triangles maintain proper topology and the new vertex’s halfedge points along the original edge direction as required.
Screenshot
The following images show the mesh before and after performing edge split operations.
The following images show the mesh after performing edge split and edge flip operations.
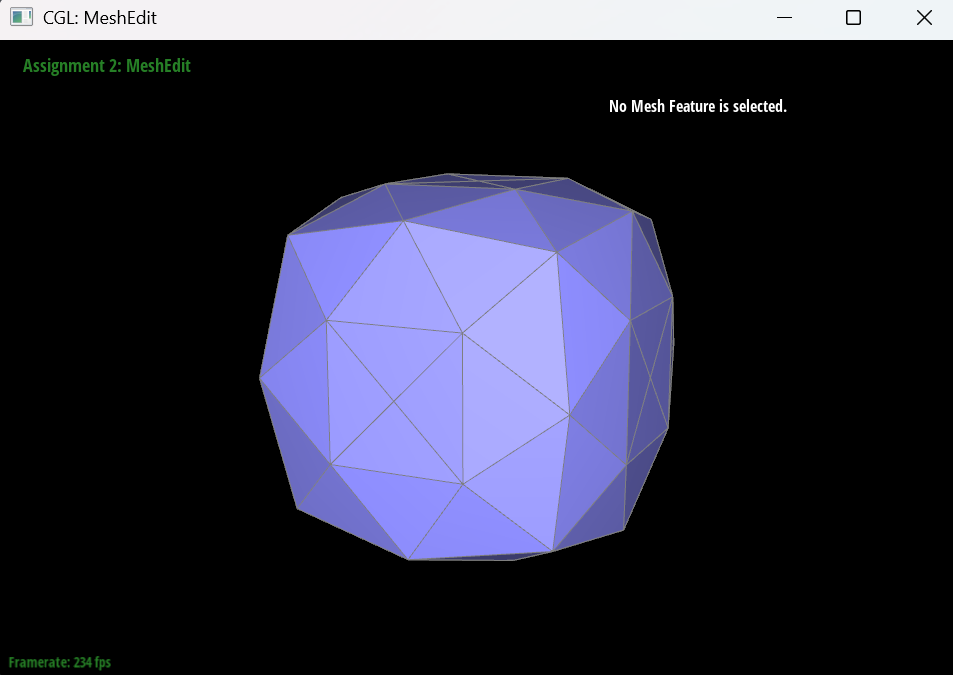
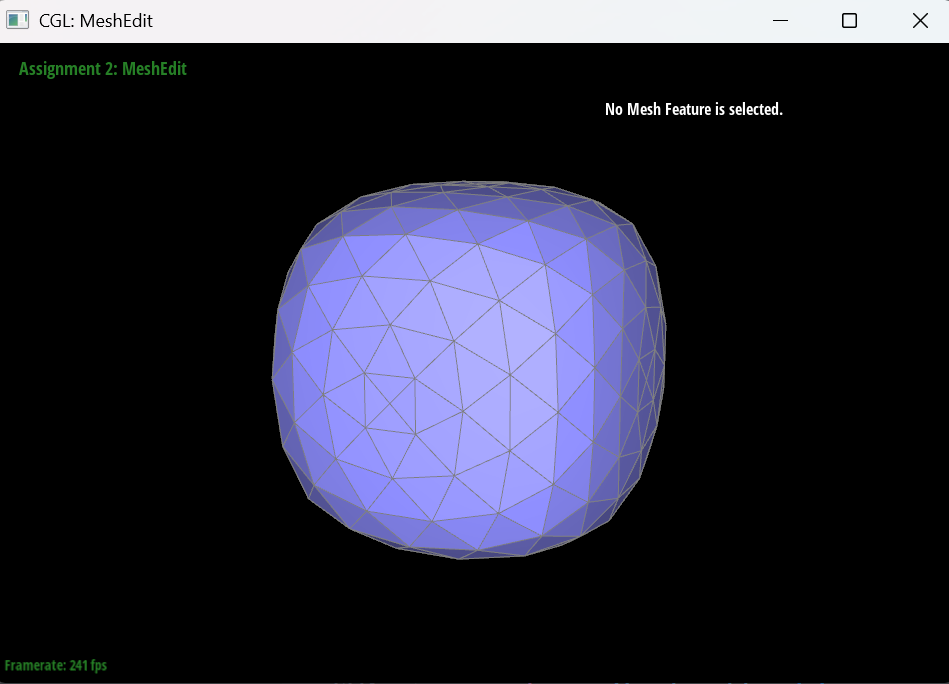
Part 6: Loop Subdivision for Mesh Upsampling
Loop subdivision is a recursive algorithm that creates smoother, more refined meshes by subdividing each triangle into four smaller triangles and adjusting vertex positions according to specific weighted averaging rules.
My implementation follows the classic five-step Loop subdivision algorithm. First, I compute new positions for all original vertices using the Loop subdivision rule, which applies different weights based on vertex degree - regular vertices (degree $6$) use the weight $\frac{3}{16}$, while irregular vertices use $\frac{3}{8n}$ where n is the degree. Second, I calculate new positions for edge midpoints using a 3:1 ratio between adjacent vertices and their opposite neighbors, with special handling for boundary edges.
The critical challenge lies in the mesh topology updates. I split every original edge to create new vertices at midpoints, carefully tracking which elements are new versus original using the isNew flags. Then I flip specific new edges that connect old and new vertices to achieve the proper Loop subdivision connectivity. A key debugging insight was to iterate over edges carefully, storing the next iterator before modification to avoid invalidated iterators. Finally, I copy all computed positions from the temporary newPosition storage to the final vertex positions, completing the subdivision process.
Results
For the torus mesh, it has sharp edges at the beginning, but after performing Loop subdivision, the mesh becomes smooth and round.
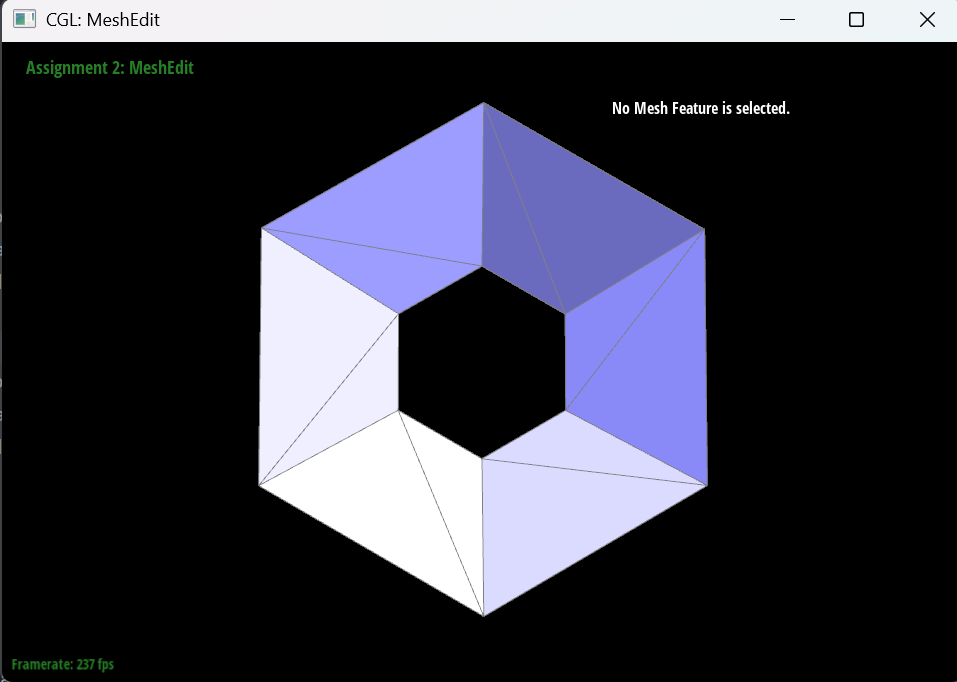
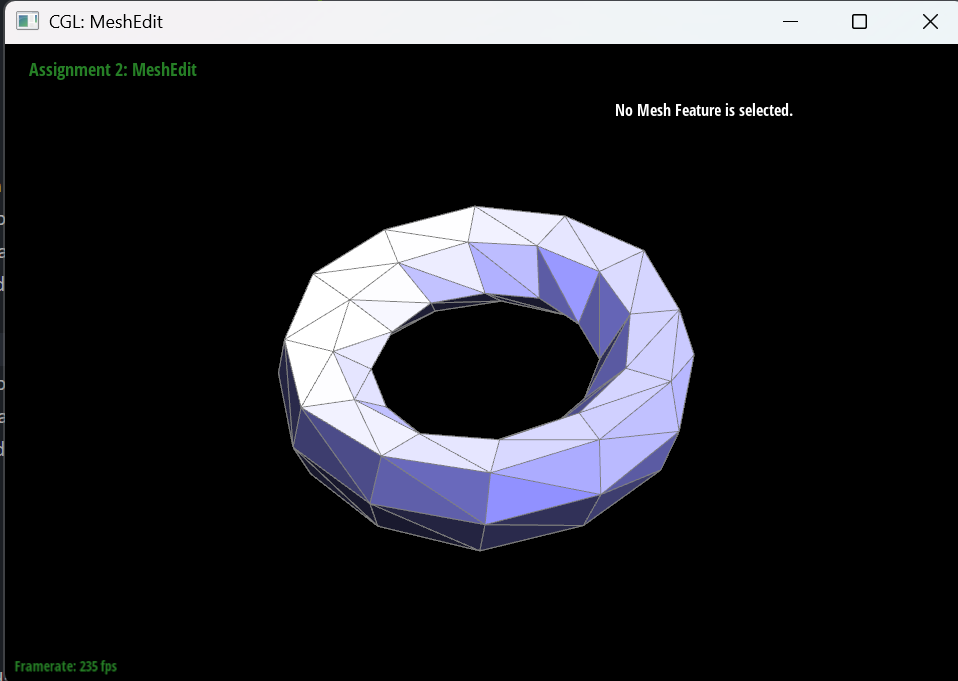
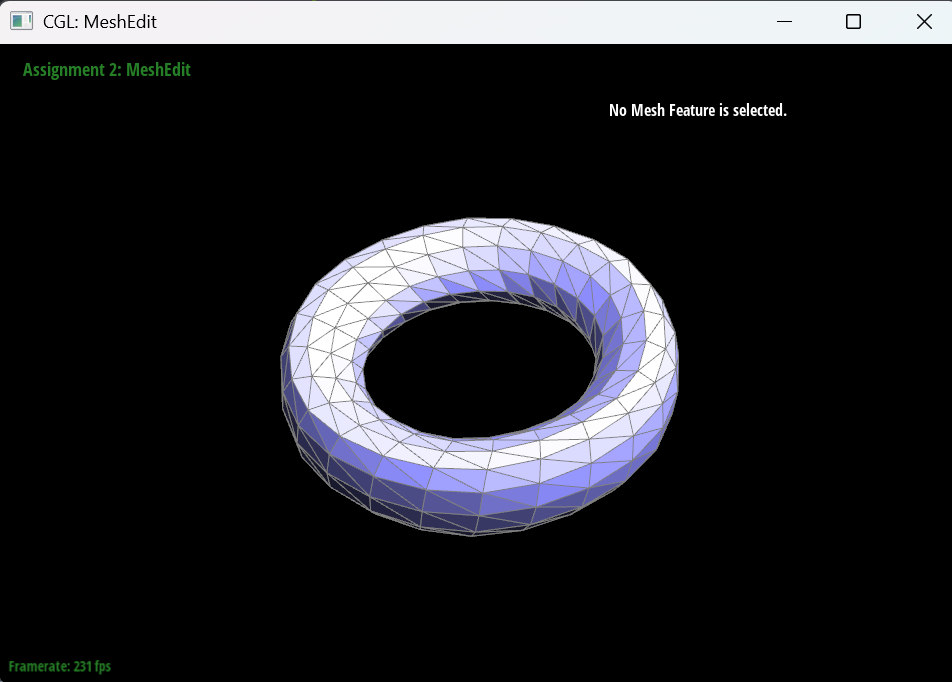
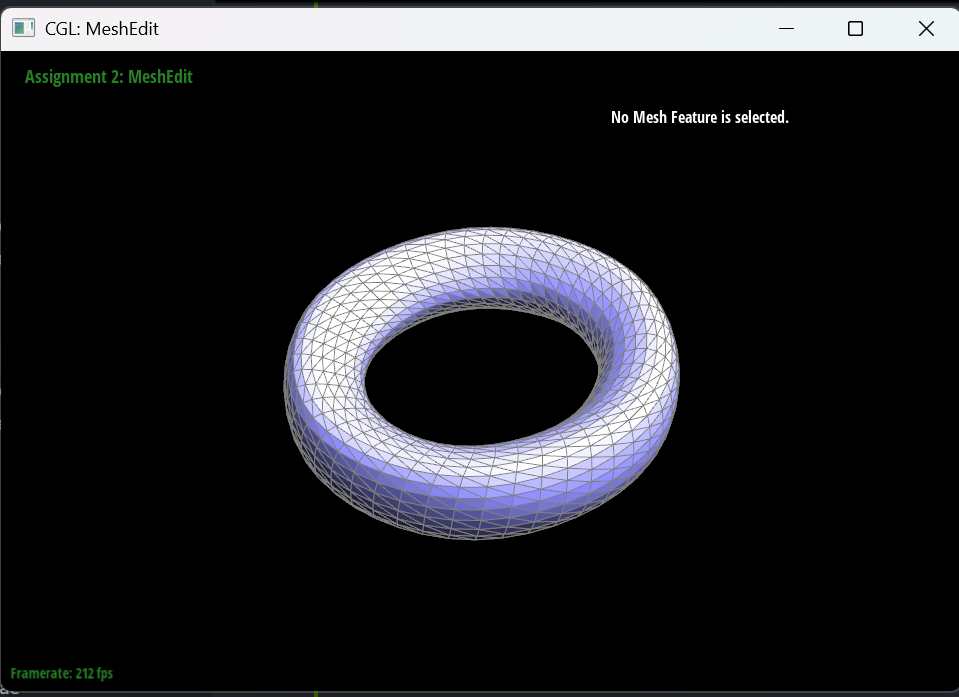
For the Cube, I split every diagonal edge in every quadrilateral face to prevent the asymmetricity issue during subdivision. In my observation, the asymmetricity is caused by the fact that the original mesh has asymmetric topology, because the square faces is not central symmetric, and the Loop subdivision algorithm magnifies this asymmetry. By splitting the diagonal edges, I ensure that the mesh has a more uniform topology, which helps to reduce the asymmetricity during subdivision.
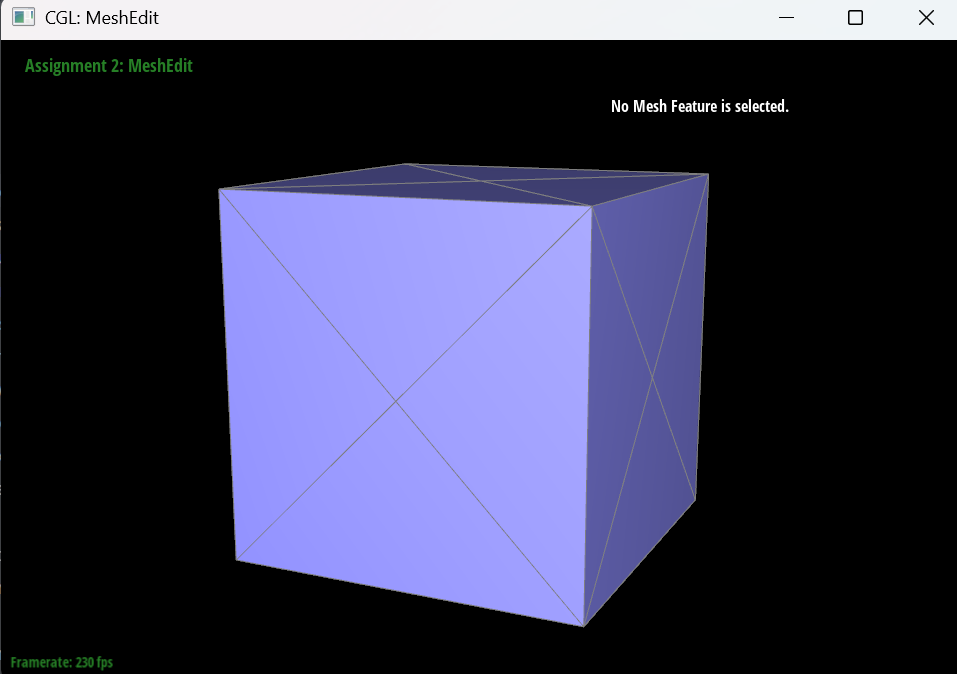
The following images show the cube mesh after performing different levels of loop subdivision.